[03-2] Understanding Linear Regression: 6 Important Assumptions
Linear regression is a powerful tool in the world of data analysis and predictive modeling. But like any tool, it comes with a set of assumptions that are crucial to ensuring the validity and reliability of your results. In this blog post, we’ll dive into the fundamental assumptions for linear regression and why they matter.
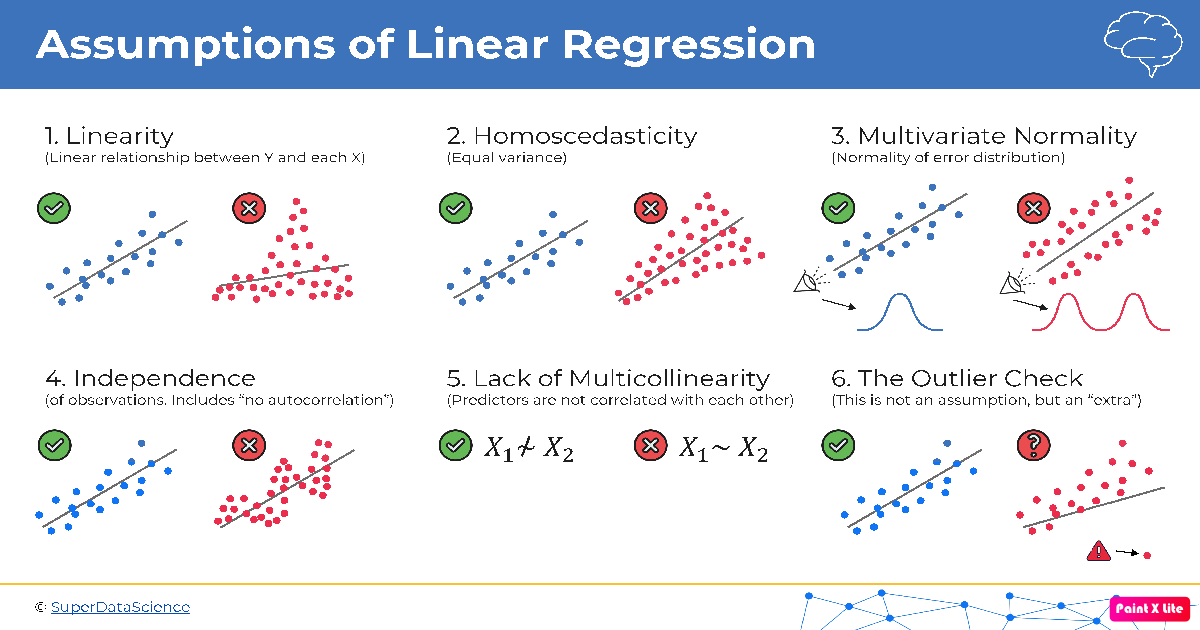
1. Linearity
The linearity assumption is at the core of linear regression. It assumes that the relationship between the independent variables and the dependent variable is linear. In other words, changes in the independent variables result in proportional changes in the dependent variable.
Here’s the formula for a simple linear regression model:
\[Y = \beta_0 + \beta_1X + \varepsilon\]We’re assuming that $Y$ and $X$ have a linear relationship.
2. Homoscedasticity
Homoscedasticity is a fancy word that essentially means the variability of the errors (residuals) should be constant across all levels of the independent variable. In other words, the spread of data points around the regression line should remain roughly the same as you move along the x-axis.
3. Multivariate Normality
This assumption involves the distribution of residuals. It’s ideal for the residuals to follow a normal distribution, meaning they’re symmetric and bell-shaped. You can check this using statistical tests or graphical methods, like a Q-Q plot.
4. Independence/No Autocorrelation
In the world of linear regression, we assume that each observation is independent of the others. Autocorrelation, also known as serial correlation, is when the residuals of a regression model are correlated with each other. This can lead to unreliable parameter estimates.
5. Lack of Multicollinearity
Multicollinearity occurs when two or more independent variables in a multiple regression model are highly correlated with each other. This can make it challenging to determine the individual effect of each variable on the dependent variable. Detecting multicollinearity can be done using correlation matrices or variance inflation factors (VIF).
6. Outlier Check
Outliers are data points that significantly differ from the rest of the data. They can heavily influence the regression model, leading to incorrect parameter estimates. Detecting outliers can be done using various graphical methods or statistical tests like the Cook’s distance.
Why Do These Assumptions Matter?
These assumptions are not arbitrary; they are the foundation of the linear regression model’s reliability. If they are violated, the model’s predictions and parameter estimates can be highly unreliable.
In practice, it’s essential to check these assumptions before interpreting the results of a linear regression analysis. If one or more assumptions are not met, you may need to transform your data, use different modeling techniques, or be cautious in interpreting the results.
Remember that real-world data rarely fits these assumptions perfectly, but being aware of them and addressing any major violations can significantly enhance the quality of your linear regression analysis.
References: